المقدمة
تشكّل الرياضيات نشاطاً فكرياً ذا أبعاد إنسانية كبرى، فهي حقل خصب لنمو الفكر النقدي، وللموضوعية والدقة والإحكام، ولتأصُّل العادة على الأمانة العلمية. إنها تقدم للطالب المعارف الضرورية في الحياة الاجتماعية، والوسائل الفعّالة لفهم واكتشاف العالم الحقيقي في شتى المجالات: الفيزياء، والكيمياء، والعلوم الطبيعية، وعلم الفلك، وعلم الاجتماع، وعلم النفس، والمعلوماتية، الخ...
إن التقدم الحثيث للعلوم والتكنولوجيا قد ترك أثراً عميقاً في المجتمع الحديث، حتى صرنا نتكلم اليوم على عصر المعلوماتية، كما كنّا نتكلم على العصر الصناعي منذ ربع قرن؛ والعالم بأسره مُجمع على أن هذا التطور ما كان ليتمّ لولا الأداة الرياضية، التي أتاح استعمالها استبدال الوصف النوعي للواقع بالبيان الكمّي والنماذج العملانية. فاليوم، وأكثر من أي وقت مضى، يتضح أن الرياضيات هي ضرورة حتمية لحياة المجتمعات وتطورها، ولا يمكن بالتالي أن تبقى حكراً على نخبة متخصصة، بل يجب أن يصبح الكثير من نتائجها ووسائلها بمتناول أكبر عدد ممكن من الأشخاص.
إن امتداد الرياضيات على مجمل الواقع، والإقبال المتزايد على تعلّمها، قد غيَّرا فيها ومن دون شك، من حيث الروح ومن حيث الاستعمال. وان النهوض في تعليمها يتم على ثلاثة محاور هي: صياغة جديدة للأهداف، وإعادة سبك للمحتوى، واختيار مناسب للطرائق.
الصياغة الجديدة للأهداف: إن الأهداف الأساسية المتعلقة بالنشاطات العقلية وبالإعداد للاستدلال الرياضي لا تزال قائمة. أما التشديد فقد تركّز بشكل خاص على العمل الشخصي في بناء الرياضيات؛ إذ لم يعد مقبولاً بأن نتعلم رياضيات معدّة سلفاً، بل أن نسهم في إعدادها بأنفسنا. وعليه، وانطلاقاً من وضعيات واقعية، حيث يثير الطلاب القضايا ويطرحون المسائل ويصوغون الفرضيات ويدققون فيها، فإن روح هذا العلم تنغرس فيهم وتتجذّر. وهدفنا أيضاً إعداد المتعلمين للتواصل: فقراءة نص رياضي وفهمه وتأويله، واستعمال الرموز والبيانات والجداول، وكتابة البرهان، وشرح الوضعيات، تبقى من الأهداف الرئيسية للتعليم.
إعادة سبك المحتوى: إن المواضيع التي تمّت معالجتها، لا يُنظر اليها من حيث فائدتها النظرية بل العملية، وينبغي أن تكون في متناول كافة الطلاب، وأن تلبي حاجاتهم في إعداد أنفسهم وفي تطورهم الثقافي. فكل مبالغة نظرية قد أبطلت، وكل مغالاة في إنجاز المهام قد أهملت؛ وهذا ما أتاح تخفيفاً واضحاً في البرامج التي ترمي في الدرجة الأولى الى إعداد "الأدمغة المنظمة". إن إدخال الآلة الحاسبة، وإمكانية استخدام الكمبيوتر هما من المستجدات التكنولوجية ذات النفع العميم في مجال الإعداد. كما إن إدراج مواضيع أخرى متعلقة بمجال المعلومات كالإحصاء مثلاً، سيسمح للأجيال الطالعة بأن تتكيف بشكل أفضل مع المسائل الاجتماعية والاقتصادية.
طرائق التدريس: إن تعليم الرياضيات يجب أن ينتظم بشكل يزيح عنها الوهم المحيط بها، ويجعلها سهلة المنال بالنسبة الى غالبية الناس. والطريقة التي ننادي بها ترمي الى الانطلاق من الوضعيات الحقيقية المعاشة أو المألوفة، لكي نثبت أن لا طلاق بين الرياضيات والواقع. وهذه الممارسة للرياضيات تقود الطالب الى فهم النماذج المجردة التي يدرك فعاليتها بفضل نجاح تآلفها مع المواضيع الأخرى.
هذا هو الإطار العام الذي على أساسه تمّ وضع هذا المنهج الجديد. وهدفنا الأساسي هو إعداد المواطن القادر تماماً على التفكير النقدي والاستقلالية الفكرية.
يرمي هذا المنهج، عبر إكساب معرفة رياضية ملائمة، الى تحقيق الأهداف العامة التالية:
إن الإعداد لبناء الحجج وتقويمها، وتنمية روح النقد، والاعداد للاستدلال الرياضي، هي من المقاصد الكبرى لهذا المنهج. لذلك يجب أن يكون المجال مفتوحاً دائماً أمام الطالب لكي: يشاهد، يحلّل، يجرّد، يشكّ، يتوقّع، يخمّن، يعمّم، يركّب، يؤوِّل، يبرهن.
إن حلّ المسائل الرياضية قد يكون النشاط الأكثر دلالة في تعليم الرياضيات. فمن جهة يجب أن تُبنى كل معرفة رياضية جديدة انطلاقاً من مسألة مطروحة، ومن جهة ثانية يجب أن يتعلم الطالب استخدام خططٍ مختلفة كي يتجاوز الصعوبات ويتوصل الى حل مسألة ما. لهذا يجب أن يكون قادراً على أن: يسلسل، يصنّف، يُكمِّم، يُوجد النماذج الرياضية، يُمارس تقنيات المحاكاة، يبني ويستخدم الخوارزميات، يتّخذ القرارات، يتحقّق، يطبّق، يقيس، يستعمل التقنيات الاستكشافية، يعالج المعلومات.
إن المجتمع الحديث بحاجة أكثر فأكثر الى يد عاملة على درجة عالية من الكفاءة، والى باحثين في كافة الميادين. ومنهج الرياضيات هذا يلبّي هذه الحاجات بإتاحة الفرصة أمام الطالب لكي: يقوم بالسعي العلمي، ينمّي روحه العلمية، يتدرّب على البحث، يقيم العلاقات بين الرياضيات والواقع المعاش بكل أبعاده، يقدر دور الرياضيات في التطور التقني والاقتصادي والثقافي.
والمقصود أيضاً اعداد الطالب للتواصل الرياضي. لهذا يجب أن يتدرب على أن: يرمِّز ويفّك رموز النصوص، يصوغ المعلومات المختلفة، ويعبِّر عنها شفهياً وخطّياً و/أو بواسطة الأدوات الرياضية.
والرياضيات هي فن فضلاً عن كونها علماً ذا فوائد تطبيقية. وهذا المنهج يتيح الفرصة أمام الطالب كي يقدرها حق قدرها، وذلك بمساعدته على أن: يكتسب الثقة بالنهج الرياضي، يقدر الدقّة والإحكام، يثمّن الترتيب والانسجام الداخلي للنظريات الرياضية، ينمّي حدسه وخياله وقدرته على الإبداع، يثابر على العمل ويحسّ بالمتعة في النشاطات الفكرية.
|
|
التعليـم الأسـاسي |
المراحـل |
||||||||||||||
|
المرحلة المتوسطة |
المرحلة الإبتدائية |
|
||||||||||||||
|
الثالثة |
الثانية |
الاولى |
|
|
|
الحلقة الثانية |
الحلقة الأولى |
الحلقـات |
||||||||
|
علوم الحياة |
علوم عامة |
اجتماع واقتصاد |
آداب وإنسانيات |
علوم |
إنسانيات |
التاسعة |
الثامنة |
السابعة |
السادسة |
الخامسة |
الرابعة |
الثالثة |
الثانية |
الاولى |
السنة المنهجية |
|
|
5 |
10 |
4 |
2 |
6 |
4 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
عدد الحصص الأسبوعية |
|
150 |
300 |
120 |
60 |
180 |
120 |
150 |
150 |
150 |
150 |
150 |
150 |
150 |
150 |
150 |
150 |
عدد الحصص السنوية |
التعليم الأساسي
|
الحساب والجبر |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الأعداد
|
|
|
|
|
2- العمليات
|
|
|
|
|
الهندسة |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الموضعة والمعلمة |
|
|
|
|
|
(10 سا) |
(5 سا) |
(5 سا) |
|
2- المجسّمات |
|
|
|
|
|
(5 سا) |
(5 سا) |
(7 سا) |
|
3- الأشكال المستوية |
|
|
|
|
|
(5 سا) |
(5 سا) |
(3 سا) |
|
4- التحويلات |
|
|
|
|
|
(5 سا) |
(5 سا) |
(5 سا) |
|
القياس |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الطول
|
|
|
|
|
|
(5 سا) |
(5 سا) |
(5 سا) |
|
2- الكتلة |
|
|
|
|
|
|
(5 سا) |
(5 سا) |
|
3- الزمن والمُدَّة |
|
|
|
|
|
|
|
(5 سا) |
|
الحساب والجبر |
|
السنة المنهجية |
الرابعة |
الخامسة |
السادسة |
|
المحور |
|
|
|
|
1- الأعداد
|
|
|
والـ 1/10.
|
|
2- العمليات |
|
|
|
|
3- التناسبية
|
|
|
|
|
|
|
|
(20 سا) |
|
4- العبارات الجبرية |
|
|
|
|
|
|
|
(20 سا) |
|
الهندسة |
|
السنة المنهجية |
الرابعة |
الخامسة |
السادسة |
|
المحور |
|
|
|
|
1- الموضعة والمعلمة |
|
|
|
|
|
(5 سا) |
(3 سا) |
(2 سا) |
|
2- المجسّمات |
|
|
|
|
|
(5 سا) |
(7 سا) |
(3 سا) |
|
3- الأشكال المستوية |
|
|
|
|
|
(5 سا) |
(5 سا) |
(5 سا) |
|
4- التحويلات |
|
|
فيها. |
|
|
(5 سا) |
(5 سا) |
(5 سا) |
|
القياس |
|
السنة المنهجية |
الرابعة |
الخامسة |
السادسة |
|
المحور |
|
|
|
|
1- الطول |
|
|
|
|
|
(6 سا) |
( 3 سا) |
|
|
2- الكتلة |
|
|
|
|
|
(3سا) |
|
|
|
3- المساحة |
|
|
|
|
|
(3 سا) |
(10سا) |
(8سا) |
|
4- الزاوية |
|
|
|
|
|
|
(2سا) |
(2سا) |
|
5- السعة |
|
|
|
|
|
(3سا) |
(5سا) |
|
|
6- الحجم |
|
|
|
|
|
|
|
(10سا) |
|
الإحصاء |
|
السنة المنهجية |
الرابعة |
الخامسة |
السادسة |
|
المحور |
|
|
|
|
1- إدارة المعلومات |
|
|
|
|
|
(5 سا) |
(5 سا) |
(5 سا) |
|
الحساب والجبر |
|
السنة المنهجية |
السابعة |
الثامنة |
التاسعة |
|
المحور |
|
|
|
|
1- الأعداد |
|
|
|
|
2- العمليات |
العامل المشترك، التحليل الى عوامل. |
|
|
|
|
(30سا) |
(5 سا) |
(10سا) |
|
3- التناسبية |
|
|
|
|
|
(10سا) |
(5 سا) |
(5 سا) |
|
4- العبارات الجبرية |
|
|
|
|
|
(15 سا) |
(20سا) |
(10سا) |
|
5- المعادلات والمتراجحات |
|
(أ س + ب)(ج س + د) = 0
|
|
|
|
(10سا) |
(15 سا) |
(40سا) |
|
الهندسة |
|
السنة المنهجية |
السابعة |
الثامنة |
التاسعة |
|
المحور |
|
|
|
|
1- الموضعة والمعلمة |
|
|
|
|
|
(10سا) |
(15 سا) |
(35 سا) |
|
2- الهندسة في الفضاء |
|
|
|
|
|
(5 سا) |
(10سا) |
(5 سا) |
|
3- الأشكال المستوية |
|
|
|
|
|
(35سا) |
(40سا) |
(20سا) |
|
4- التحويلات والمتجهات |
|
|
|
|
|
(5سا) |
(5سا) |
(5سا) |
|
5- حساب المثلّثات |
|
|
|
|
|
|
|
(5سا) |
|
الإحصاء |
|
السنة المنهجية |
السابعة |
الثامنة |
التاسعة |
|
المحور |
|
|
|
|
1- إدارة المعلومات |
|
|
|
|
|
(5سا) |
(10سا) |
(10سا) |
التعليم الأساسي - المرحلة الابتدائية - الحلقة الأولى
يجب على منهج الرياضيات أن يجعل المتعلّم قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يتعرف الى الاتجاهات أو العلاقات في متتاليات من الوقائع البسيطة.
يبرر إجابة ما.
ب- حل المسائل:
يقوم بالمبادرات.
يستخدم التقنيات الرياضية الملائمة لحل المسائل في الحياة العادية.
يستخدم الوسائل الاستكشافية ليجد نتيجة ما.
ج- التواصل:
يستخدم التمثيلات الصورية أو الرمزية.
يعبّر عمّا يريد بشكل صحيح شفهياً أو خطياً.
يطرح أسئلة ويجيب عن أخرى.
د- الفضاء:
يتوجّه بواسطة الخارطة.
يتعرف الى المجسّمات والى الأشكال المستوية.
ه- العدد:
يتعرف الى الأعداد الطبيعية ويستخدم الترقيم الهندي العربي.
يتعرف الى العمليات الحسابية الأربع.
يتقن التقنيات الإجرائية للجمع والطرح.
يتدرَّب على التقنيات الإجرائية للضرب والقسمة.
يطبّق العلاقات بين الأعداد لإجراء الحساب الذهني.
يستخدم الكسور البسيطة للدلالة على الحصص.
و- القياس:
يجري قياسات الطول والكتلة والزمن.
يقرأ الساعة.
المحتوى |
|
|
الحساب والجبر (120 سا) 1. الأعداد الطبيعية (60 سا)
2. الجمع (50 سا)
3. الطرح (10 سا)
|
الهندسة (25 سا) 1- الموضعة والمعلمة (10 سا)
2. المجسّمات (5 سا)
3. الأشكال المستوية (5 سا)
4. التحويلات (5 سا)
القياس (5 سا) 1. الطول (5 سا)
|
المحتوى |
|
|
الحساب والجبر (120 سا) 1. الأعداد الطبيعية (25 سا)
2. الجمع (30 سا)
3. الطرح (30 سا)
4. الضرب (30 سا)
5. القسمة (5 سا)
|
الهندسة (20 سا) 1. الموضعة والمعلمة (5 سا)
2. المجسّمات (5 سا)
3. الأشكال المستوية (5 سا)
4. التحويلات (5 سا)
القياس (10سا)1. الطول (5 سا)
2. الكتلة (5 سا)
|
المحتوى |
|
|
الحساب والجبر (110 سا) 1. الأعداد الطبيعية (15 سا)
2. الكسور (5 سا)
3. الجمع (10 سا)
4. الطرح (20 سا)
5. الضرب (30 سا)
6. القسمة (30 سا)
|
الهندسة (20 سا) 1. الموضعة والمعلمة (5 سا)
2. المجسّمات (7 سا)
3. الأشكال المستوية (3 سا)
4. التحويلات (5 سا)
القياس (20 سا) 1. الطول (10 سا)
2. الكتلة (5 سا)
3. الزمن والمدة (5 سا)
|
التعليم الأساسي - المرحلة الابتدائية - الحلقة الثانية
بالنسبة الى المتعلّمين الذين ينهون هذه الحلقة الدراسية، يتوخى المنهج تزويدهم بالإعداد اللازم والثابت، بحيث يكون الذين يجبرون منهم على ترك المدرسة في سن الثانية عشرة ليشاركوا في الانتاج، قد تلقوا وأتقنوا تأهيلاً يعصمهم من العودة الى الأميّة في الرياضيات. وهكذا يجب أن يكون المتعلّم قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يجد الاتجاهات في متتاليات من النتائج ويعممها.
يستخلص تقارير عامة انطلاقاً من تحقيقات فعلية.
يثبت الطرائق.
يقيم الحجج عن طريق القياس، وبضرب الأمثال والأمثال المضادة.
ب- حل المسائل:
يمثّل الوضعيات ويعالج المعلومات.
يستخدم ويطبّق الرياضيات في مختلف المجالات، لا سيما في التكنولوجيا وفي الفروع الأخرى للمعرفة.
يتحقق من النتائج.
يستخدم الآلة الحاسبة لإجراء العمليات الحسابية الأربع.
ج- التواصل:
يقرأ، ويفهم ويؤوّل نصاً رياضياً بترجمته الى أشكال أو تمثيلات أو معادلات.
يترجم الى اللغة المحكية علاقة رياضية معطاة.
د- الفضاء:
يمثّل المواقع على الخارطة.
يحدّد الأشكال المستوية المختلفة ويستخدم الأدوات الهندسية لتمثيلها.
يحقّق بسط بعض المجسمات.
ه- العدد:
يتقن نظام الترقيم الهندي العربي.
يتعرّف الى الأعداد العشرية.
يتقن جميع نماذج الحساب: المؤخر، الذهني، وبواسطة الآلة الحاسبة (الأعداد الطبيعية والعشرية).
يجري العمليات البسيطة على الكسور.
يقدِّر نتيجة ما.
و- القياس:
يجري قياسات المحيط، المساحة، السعة والزاوية.
يستخدم الوحدات المترية.
ز- الإحصاء:
يبوِّب ويؤوِّل المعلومات.
المحتوى |
|
|
الحساب والجبر (110 سا) 1. الأعداد الطبيعية (15 سا)
2. الكسور (15 سا)
3. الأعداد العشرية (10 سا)
4. الجمع (15 سا)
5. الطرح (15 سا)
6. الضرب (10 سا)
7. القسمة (30 سا)
|
الهندسة (20 سا) 1. الموضعة والمعلمة (5 سا)
2. المجسّمات (5 سا)
3. الأشكال المستوية (5 سا)
4. التحويلات (5 سا)
القياس (15 سا) 1. الطول (6 سا)
2. الكتلة (3 سا)
3. المساحة (3 سا)
4. السعة (3 سا)
الإحصاء (5 سا)1. إدارة المعلومات (5 سا)
|
المحتوى |
|
|
الحساب والجبر (100 سا) 1. الأعداد الطبيعية (20 سا)
2. الكسور (10 سا)
3. الأعداد العشرية (10 سا)
4. الجمع (15 سا)
5. الطرح (15 سا)
6. الضرب (20 سا)
7. القسمة (10 سا)
|
الهندسة (25 سا) 1. الموضعة والمعلمة (3 سا)
2. المجسّمات (7 سا)
3. الأشكال المستوية (10 سا)
4. التحويلات (5 سا)
القياس (20 سا) 1. الطول (3 سا)
2. المساحة (10 سا)
3. الزاوية (2 سا)
4. السعة (5 سا)
الإحصاء (5 سا) 1. إدارة المعلومات (5 سا)
|
المحتوى |
|
|
الحساب والجبر (110سا) 1. الأعداد الطبيعية (15 سا)
2. الكسور (10 سا)
3. الأعداد العشرية (10 سا)
4. الأعداد النسبية (15 سا)
5. الجمع (5 سا)
6. الطرح (5 سا)
7. الضرب (10 سا)
8. القسمة (10 سا)
9. التناسبية (20 سا)
10. العبارات الجبرية (10 سا)
|
الهندسة (25سا) 1. الموضعة والمعلمة (2 سا)
2. المجسّمات (3 سا)
3. الأشكال المستوية (10 سا)
4. التحويلات (10 سا)
القياس (20سا)1. المساحة (8 سا)
2. الزاوية (2 سا)
3. الحجم (10 سا)
الإحصاء (5 سا)1. إدارة المعلومات (5 سا)
|
التعليم الأساسي - المرحلة المتوسطة
يهدف هذا المنهج الى أن يكون المتعلّم قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يربط مشاهدات الواقع الى تمثيلات وهذه الأخيرة الى مفاهيم.
يستقرئ الحد العام لمتتالية من النتائج، مبنيَّة حسب الأصول.
يميّز بين تقرير عام وتقرير خاص.
يجري براهين بسيطة.
يتعرّف الى برهان خاطئ.
ب- حل المسائل:
يحلّل وضعية ما كي يستنتج منها العناصر الوثيقة الصلة بالموضوع.
يستقصي المعلومات اللازمة لإيضاح معطى غير وافٍ.
يبني نموذجاً رياضياً مرتبطاً بوضعية ما.
يختار خطة ليجد الحل.
يفكّك صعوبة ما الى أعمال أكثر بساطة، وبالعكس يدمج الوقائع اللازمة كي يستنتج.
يستخدم الآلات الحاسبة ذات الذاكرة.
ج- التواصل:
يقرأ، يفهم ويستخدم الرموز واللغة الرياضية.
يعرض نتاجه بوضوح وإحكام شفهياً وخطياً، ويوجه عناية خاصة الى كتابة البرهان.
د- الفضاء:
يبني الأشكال الهندسية انطلاقاً من المعطيات.
يمثل المجسّمات.
يبرهن ويطبق خصائص الأشكال المستوية.
يجري التحويلات التآلفية على الأشكال.
ه- العدد:
يجد ويستخدم العلاقات بين الأعداد.
يسحب التقنيات الإجرائية على العبارات الحرفية.
يجد القيم التقريبية لنتيجة ما.
و- القياس:
يجري قياسات المساحات والحجوم.
ز- الإحصاء:
يقوم بتمثيل المعلومات الإحصائية ويقرأ التمثيلات.
يحسب متوسط توزيع إحصائي.
المحتوى |
|
|
الحساب والجبر (90سا) 1. الأعداد الطبيعية (10 سا)
2. الكسور (10 سا)
3. الأعداد العشرية (5 سا)
4. العمليات (30 سا)
5. التناسبية (10 سا)
6. العبارات الجبرية (15 سا)
7. المعادلات والمتراجحات (10 سا)
|
الهندسة (55سا) 1. الموضعة والمعلمة (10 سا)
2. المجسّمات (5 سا)
3. الأشكال المستوية (35 سا)
4. التحويلات (5 سا)
الإحصاء (5 سا)1. إدارة المعلومات (5 سا)
|
المحتوى |
|
|
الحساب والجبر (70سا) 1. الأعداد الطبيعية (5 سا)
2. الكسور (10 سا)
3. الأعداد العشرية (5 سا)
4. الجذور التربيعية (10 سا)
5. العمليات (5 سا)
6. التناسبية (5 سا)
7. العبارات الجبرية (20 سا)
8. المعادلات والمتراجحات (15 سا)
|
الهندسة (70سا) 1. الموضعة والمعلمة (15 سا)
2. الهندسة في الفضاء (10 سا)
3. الأشكال المستوية (40 سا)
4. التحويلات والمتجهات (5 سا)
الإحصاء (10سا)1. إدارة المعلومات (10 سا)
|
المحتوى |
|
|
الحساب والجبر (70سا) 1. الأعداد الحقيقية (5 سا)
2. العمليات (10 سا)
3. التناسبية (5 سا)
4. العبارات الجبرية (10 سا)
5. المعادلات والمتراجحات (40 سا)
|
الهندسة (70سا) 1. الموضعة والمعلمة (35 سا)
2. الهندسة في الفضاء (5 سا)
3. الأشكال المستوية (20 سا)
4. التحويلات والمتجهات (5 سا)
5. حساب المثلثات (5 سا)
الإحصاء (10سا)1. إدارة المعلومات (10 سا)
|
التعليم الثانوي – فرع الآداب والإنسانيات
في هذا الفرع يدرك المتعلّم أهمية الرياضيات كنشاط فكري أساسي، ويستخدم نتائجها لمعالجة المعلومات التي يقع عليها في الآداب والعلوم الإنسانية. لذلك يجب أن يكون قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يتعرّف الى مختلف أشكال الاستدلال الرياضي.
ب- حل المسائل:
يستخدم تأويلاً رياضياً ملائماً لتمثيل معطيات مسألة ما.
يجد الحل لمسألة ما متبعاً خوارزمية معطاة.
ج- التواصل:
يبيّن القواعد والعلاقات في نص رياضي.
يكتب نتاجه بإحكام.
د- الفضاء:
يمثّل المجسّمات.
ه- العدد والجبر:
يحلّل أسباب توسيع مجموعات الأعداد ط ص ن ح.
يعمّم المفاهيم الأساسية التي استعملها سابقاً مثل: المجموعة، العلاقة، قانون التشكيل وحساب الجمل.
يكتسب مفهوم بنية الزمرة.
يحل المسائل البسيطة ذات المتغيّر الواحد أو المتغيرين.
و- التحليل:
يدرس ويمثل التوابع البسيطة.
يربط ما بين التزايد الأسي والتابع الأسي.
يحسب الفوائد البسيطة أو المركبة.
ز- الإحصاء والاحتمال:
ينظّم المعلومات بتمثيلها بيانياً.
يدرس مميزات متسلسلة إحصائية ذات صفة واحدة.
يحل المسائل البسيطة في الاحتمالات، خاصة في الحالة المنفصلة حيث الحوادث متساوية الاحتمال.
|
الجبر |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- المرتكزات |
|
|
|
|
|
(7سا) |
(10سا) |
(10سا) |
|
2- الحساب العددي والحرفي |
الحقيقي.
|
|
|
|
|
(23سا) |
(10سا) |
|
|
3- المعادلات والمتراجحات |
والمنطوية على قيمة مطلقة.
وتأويله هندسياً. |
|
|
|
|
(15سا) |
(15سا) |
(10سا) |
|
4- كثيرات الحدود |
|
|
|
|
|
(8سا) |
(5سا) |
|
|
5- الأعداد |
|
|
|
|
|
(2سا) |
|
|
|
الهندسة |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الدراسة التقليدية |
المألوفة.
التوازي. |
|
|
|
|
(17سا) |
|
|
|
2- الدراسة المتجهية |
|
|
|
|
|
(20سا) |
|
|
|
3- الدراسة التحليلية |
|
|
|
|
|
(18سا) |
|
|
|
التحليل (التوابع العددية) |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- التعاريف والتمثيل |
|
المقاربة الرأسية والأفقية.
|
|
|
|
(20سا) |
(15سا) |
(15سا) |
|
2- الاتصال والاشتقاق |
|
الحساب.
|
|
|
|
|
(25سا) |
|
|
3- التكامل |
|
|
|
|
|
|
(10سا) |
|
|
4- النماذج الرياضية لزوم الاقتصاد والعلوم الاجتماعية |
|
|
|
|
|
|
|
(10سا) |
|
حساب المثلثات |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الخطوط المثلّثية |
|
|
|
|
|
(10سا) |
|
|
|
الإحصاء والاحتمال |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الإحصاء |
منفصلة.
|
|
|
|
|
(10سا) |
(15سا) |
(10سا) |
|
2- الاحتمال |
|
المتساوية الاحتمال.
|
|
|
|
|
(15سا) |
(5سا) |
التعليم الثانوي - فرع الاجتماع والاقتصاد
في هذا الفرع على المتعلّم أن يدرك أهمية الرياضيات كأداة لا بد منها لمعالجة المعلومات المستقاة من علم الاقتصاد ومن العلوم الاجتماعية. لذلك يجب أن يكون قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يتعرّف الى الفرق بين التأويل الرياضي والبديهيات المحسوسة أو التجريبية.
يضع المخمّنات ويتخيل وسيلة لاختبارها.
ب- حلّ المسائل:
يصوغ مسألة انطلاقاً من وضعيات مطروحة في الاقتصاد وفي العلوم الاجتماعية.
يستخدم تأويلاً رياضياً ملائماً لتمثيل معطيات مسألة ما.
يطبق معارفه الرياضية ليجد حل مسألة ما، متّبعاً خوارزمية مناسبة.
يناقش مدى صحة الحلول الناتجة.
ج- التواصل:
يفهم وثيقة رياضية أطلع عليها، ويحفظ منها النقاط الأساسية.
يدوّن الملاحظات أثناء عرض رياضي.
د- الفضاء:
يبرهن ويطبّق خصائص المجسّمات.
ه- العدد والجبر:
يحلّل أسباب توسيع مجموعات الأعداد ط ص ن ح.
يعمّم مفاهيم أساسية استخدمها سابقاً مثل: المجموعة، العلاقة، قانون التشكيل.
يكتسب مفهوم بنية الزمرة.
يطور الأدوات الرياضية للحساب العددي، ولحلّ نظام معادلات أو متراجحات.
و- التحليل:
يستخدم ويؤوِّل بيانياً مفاهيم النهاية والاتصال والاشتقاق، بغية دراسة التوابع العددية.
يحلّل بيانات التوابع: كثيرة الحدود، المُنْطَقة، الصماء، المثلثية، اللوغاريتمية، والأسِّية.
يكامل التابع، ويحل المعادلات التفاضلية البسيطة.
يحل معادلات الفروق المنتهية.
يدرس التوابع ذات الصلة بالاقتصاد أو الاجتماع.
يحل مسائل من الرياضيات المالية.
ز- الإحصاء والاحتمال:
ينظم المعلومات بتمثيلها بيانياً.
يدرس مميزات متسلسلة إحصائية ذات صفة واحدة أو صفتين.
يحل المسائل البسيطة في الاحتمالات، خاصة في الحالة المنفصلة حيث الحوادث متساوية الاحتمال.
|
الجبر |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- المرتكزات |
|
|
|
|
|
(7سا) |
(10سا) |
(8سا) |
|
2- الحساب العددي والحرفي |
الحقيقي.
|
|
|
|
|
(23سا) |
(10سا) |
(7سا) |
|
3- المعادلات والمتراجحات |
والمنطوية على قيمة مطلقة.
|
|
|
|
|
(15سا) |
(15سا) |
(10سا) |
|
4- كثيرات الحدود |
|
|
|
|
|
(8سا) |
(5 سا) |
|
|
5- الأعداد |
|
|
|
|
|
(2سا) |
|
|
|
الهندسة |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الدراسة التقليدية |
المألوفة.
التوازي. |
|
|
|
|
(17 سا) |
|
|
|
2- الدراسة المتجهية |
|
|
|
|
|
(20 سا) |
|
|
|
3- الدراسة التحليلية |
|
|
|
|
|
(18 سا) |
|
|
|
التحليل (التوابع العددية) |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- التعاريف والتمثيل |
|
|
اللوغاريتم للأساس د.
|
|
|
(20 سا) |
(15سا) |
)20 سا) |
|
2- الاتصال والاشتقاق |
|
|
|
|
|
|
(25 سا) |
(5 سا) |
|
3- التكامل |
|
|
|
|
|
|
(10 سا) |
(10 سا) |
|
4- المعادلات التفاضلية |
|
|
|
|
|
|
|
(10 سا) |
|
5- النماذج الرياضية لزوم الاقتصاد والعلوم الاجتماعية |
|
|
|
|
|
|
|
(15 سا) |
|
حساب المثلثات |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1. الخطوط المثلّثية |
|
|
|
|
|
(10 سا) |
|
|
|
الإحصاء والاحتمال |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الإحصاء |
|
|
|
|
|
(10 سا) |
)15 سا) |
(15 سا) |
|
2- الاحتمال |
|
|
|
|
|
|
(15 سا) |
(20 سا) |
التعليم الثانوي - فرع العلوم العامة
إن هذا الفرع يزوّد الطلاب بإعداد رياضي رفيع، بقصد تهيئتهم لمتابعة دراساتهم العليا كمعلمين أو مهندسين أو باحثين. لذلك يجب أن يكون الطالب قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يتعرف الى الفرق بين التأويل الرياضي والبديهيات المحسوسة أو التجريبية.
يضع المخمّنات ويتخيل وسيلة لاختبارها.
يجري البراهين مستخدماً أنواعاً مختلفة من الاستدلال.
يحلل ويبرهن تقريراً بالشرط اللازم والكافي.
يتعرّف الى تقرير كلي، وتقرير وجود وتقرير وحدانية.
يقوّم حجة رياضية وينقد برهاناً.
يجري برهاناً بطريقة الاستقراء.
ب- حل المسائل:
يصوغ مسألة انطلاقاً من وضعيات مطروحة في الرياضيات وفي العلوم الأخرى، أو عارضةٍ في الحياة العادية.
يستخدم تأويلات رياضية مختلفة لتمثيل معطيات مسألة ما، ثم يتخيل خطة ملائمة لحلها؛ كما يجري مقاربات مختلفة لتحقيق هذه الخطة مستخدماً معارفه الرياضية في ذلك.
يناقش مدى صحة الحلول الناتجة.
ج- التواصل:
يقدِّم عرضاً حول وثيقة رياضية إطّلع عليها.
يدوِّن الملاحظات أثناء عرض رياضي.
يجري نقداً لطرح رياضي.
يصوغ برهاناً بطريقة صحيحة.
د- الفضاء:
يبرهن ويطبّق خصائص المجسّمات والقطوع المخروطية.
يحدد الأشكال المستوية أو الفضائية مستخدماً المفاهيم المتجهية.
يدرس تحليلياً مسائل هندسية.
يحدد آثار التحويلات على الأشكال المستوية.
ه- العدد والجبر:
يحلّل أسباب توسيع مجموعات الأعداد ط ص ن ح ك.
يدرس خصائص الأعداد المركبة واستخداماتها في الهندسة وفي حساب المثلّثات.
يعمّم مفاهيم أساسية استخدمها سابقاً مثل: المجموعة، العلاقة، قانون التشكيل وحساب الجمل.
يكتسب مثالاً عن البنية.
يطور الأدوات الرياضية للحساب العددي، ولحل نظام معادلات أو متراجحات.
و- التحليل:
يكتسب المفاهيم الأساسية للنهاية والاتصال والاشتقاق، ويستخدمها كي يمثل هندسياً تغيرات تابع عددي.
يحلل بيانات التوابع: كثيرة الحدود، المُنْطَقة، الصماء، المثلثية، اللوغاريتمية، والأسِّية.
يكامل التابع، ويحل المعادلات التفاضلية البسيطة.
ز- الإحصاء والاحتمال:
ينظم المعلومات بتمثيلها بيانياً.
يدرس مميزات متسلسلة إحصائية ذات صفة واحدة.
يحل المسائل البسيطة في الاحتمالات، خاصة في الحالة المنفصلة حيث الحوادث متساوية الاحتمال.
|
الجبر |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- المرتكزات |
|
|
|
|
|
(7 سا) |
(6 سا) |
(15 سا) |
|
2- الحساب العددي والحرفي |
الحقيقي.
|
|
|
|
|
(23 سا) |
)6 سا) |
(10 سا) |
|
3- المعادلات والمتراجحات |
والمنطوية على قيمة مطلقة.
|
|
|
|
|
(15 سا) |
(20 سا) |
(10 سا) |
|
4- كثيرات الحدود |
|
|
|
|
|
(8 سا) |
(4 سا) |
|
|
5- الأعداد |
|
|
|
|
|
(2 سا) |
(8 سا) |
(25 سا) |
|
الهندسة |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الدراسة التقليدية |
|
|
|
|
|
(17 سا) |
(18 سا) |
(20 سا) |
|
2- الدراسة المتجهية |
|
|
(
|
|
|
(20 سا) |
(16 سا) |
(5 سا) |
|
3- الدراسة التحليلية |
|
|
|
|
|
(18 سا) |
(9 سا) |
(30 سا) |
|
4- التحويلات المستوية |
|
|
|
|
|
|
(16 سا) |
(35 سا) |
|
التحليل (التوابع العددية) |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- التعاريف والتمثيل |
|
|
|
|
|
(20 سا) |
(14 سا) |
(40 سا) |
|
2- الاتصال والاشتقاق |
|
|
|
|
|
|
(22 سا) |
(25 سا) |
|
3- التكامل |
|
|
|
|
|
|
(6 سا) |
(30 سا) |
|
4- المعادلات التفاضلية |
|
|
|
|
|
|
|
(10 سا) |
|
حساب المثلثات |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الخطوط المثلّثية |
|
|
|
|
|
(10 سا) |
(4 سا) |
(5 سا) |
|
2- المعادلات المثلّثية |
|
|
|
|
|
|
(7 سا) |
(5 سا) |
|
3- التوابع الدائرية |
|
|
|
|
|
|
(4 سا) |
(5 سا) |
|
الإحصاء والاحتمال |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الإحصاء |
|
|
|
|
|
(10 سا) |
(8 سا) |
(10 سا) |
|
2- الاحتمال |
|
|
|
|
|
|
(12 سا) |
(20 سا) |
التعليم الثانوي - فرع علوم الحياة
في هذا الفرع يتلقى المتعلّمون إعدادا راسخاً في الرياضيات، ومعارف ضرورية لفهم ومعالجة المسائل التي يصادفونها في العلوم التجريبية وفي الحياة العادية. لذلك يجب أن يكون المتعلّم قادراً في المجالات التالية على أن:
أ- الاستدلال الرياضي:
يتعرف الى الفرق بين التأويل الرياضي والبديهيات المحسوسة أو التجريبية.
يضع المخمّنات ويتخيّل وسيلة لاختبارها.
يجري البراهين مستخدماً أنواعاً مختلفة من الاستدلال.
يتعرّف الى تقرير كلي، وتقرير وجود وتقرير وحدانية.
ب- حل المسائل:
يصوغ مسألة انطلاقاً من وضعيات مطروحة في العلوم الأخرى.
يستخدم وسائل رياضية ملائمة لتمثيل معطيات مسألة ما.
يطبق معارفه الرياضية ليجد حل مسألة ما، متبعاً خطة مناسبة.
ج- التواصل:
يفهم وثيقة رياضية أطلع عليها، ويحفظ منها النقاط الأساسية.
يدوّن الملاحظات أثناء عرض رياضي.
يصوغ برهاناً بطريقة صحيحة.
د- الفضاء:
يبرهن ويطبّق خصائص المجسّمات.
يستخدم المفاهيم المتجهية، كأداة للدراسة في مواد مختلفة.
يدرس تحليلياً مسألة هندسية.
ه- العدد والجبر:
يحلّل أسباب توسيع مجموعات الأعداد ط ص ن ح ك.
يدرس خصائص الأعداد المركبة.
يعمّم مفاهيم أساسية استخدمها سابقاً مثل: المجموعة، العلاقة وقانون التشكيل.
يكتسب مفهوم بنية الزمرة.
يطور الأدوات الرياضية للحساب العددي، ولحل نظام معادلات أو متراجحات.
و- التحليل:
يكتسب المفاهيم الأساسية للنهاية والاتصال والاشتقاق، ويستخدمها ليقوم بدراسة بيانية للعلاقات التوابع المتأتّية من العلوم الأخرى.
يحلّل بيانات التوابع: كثيرة الحدود، المُنْطَقة، الصماء، المثلثية، اللوغاريتمية والأسِّية.
يكامل التابع، ويحل المعادلات التفاضلية البسيطة.
ز- الإحصاء والاحتمال:
ينظم المعلومات بتمثيلها بيانياً.
يدرس مميزات متسلسلة إحصائية ذات صفة واحدة.
يحلّ المسائل البسيطة في الاحتمالات، خاصة في الحالة المنفصلة حيث الحوادث متساوية الاحتمال.
يسن قانوناً في الاحتمال في حالة بسيطة، ويشرح مميزاته.
|
الجبر |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- المرتكزات |
|
|
|
|
|
(7 سا) |
(6 سا) |
(8 سا) |
|
2- الحساب العددي والحرفي |
|
|
|
|
|
(23 سا) |
(6 سا) |
(10 سا) |
|
3- المعادلات والمتراجحات |
|
|
|
|
|
(15 سا) |
(20 سا) |
(7 سا) |
|
4- كثيرات الحدود |
|
|
|
|
|
(8 سا) |
(4 سا) |
|
|
5- الأعداد |
|
|
|
|
|
(2 سا) |
(8 سا) |
(10 سا) |
|
الهندسة |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الدراسة التقليدية |
|
|
|
|
|
(17 سا) |
(18 سا) |
|
|
2- الدراسة المتجهية |
|
|
|
|
|
(20 سا) |
(16 سا) |
|
|
3- الدراسة التحليلية |
|
|
|
|
|
(18 سا) |
(9 سا) |
(15 سا) |
|
4- التحويلات المستوية |
|
|
|
|
|
|
(16 سا) |
|
|
التحليل (التوابع العددية) |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- التعاريف والتمثيل |
|
|
|
|
|
(20 سا) |
(14 سا) |
(25 سا) |
|
2- الاتصال والاشتقاق |
|
|
|
|
|
|
(22 سا) |
(15 سا) |
|
3- التكامل |
|
|
|
|
|
|
(6 سا) |
(15 سا) |
|
4- المعادلات التفاضلية |
|
|
|
|
|
|
|
(10 سا) |
|
حساب المثلثات |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الخطوط المثلّثية |
|
|
|
|
|
(10 سا) |
(4 سا) |
|
|
2- المعادلات المثلّثية |
|
|
|
|
|
|
(7 سا) |
|
|
3- التوابع الدائرية |
|
|
د جتا (ب س + هـ) وَ د جا (ب س + هـ) |
|
|
|
(4 سا) |
(5 سا) |
|
الإحصاء والاحتمال |
|
السنة المنهجية |
الأولى |
الثانية |
الثالثة |
|
المحور |
|
|
|
|
1- الإحصاء |
|
|
|
|
|
(10 سا) |
(8 سا) |
(10 سا) |
|
2- الاحتمال |
|
|
|
|
|
|
(12 سا) |
(20 سا) |
المحتوى |
|
|
الجبر (55 سا) 1. المرتكزات (7 سا)
2. الحساب العددي والحرفي (23 سا)
3. المعادلات والمتراجحات (15 سا)
4. كثيرات الحدود (8 سا)
5. الأعداد (2 سا)
|
الهندسة (55 سا) 1. الدراسة التقليدية (17 سا)
2. الدراسة المتجهية (20 سا)
3. الدراسة التحليلية (18 سا)
التحليل (التوابع العددية) (20 سا) 1. التعاريف والتمثيل (20 سا)
حساب المثلثات (10 سا) 1. الخطوط المثلّثية (10 سا)
الإحصاء (10 سا)1. الإحصاء (10 سا)
|
المحتوى |
|
|
الجبر (40 سا) 1. المرتكزات (10 سا)
2. الحساب العددي والحرفي (10 سا)
3. المعادلات والمتراجحات (15 سا)
4. كثيرات الحدود (5 سا)
التحليل (التوابع العددية) (50 سا) 1. التعاريف والتمثيل (15 سا)
2. الاتصال والاشتقاق (25 سا)
3. التكامل (10سا)
|
الإحصاء والاحتمال (30 سا)1. الإحصاء (15 سا)
2. الاحتمال (15 سا)
|
المحتوى |
|
|
الجبر (44 سا) 1. المرتكزات (6 سا)
2. الحساب العددي والحرفي (6 سا)
3. المعادلات والمتراجحات (20 سا)
4. كثيرات الحدود (4 سا)
5. الأعداد (8 سا)
الهندسة (59 سا) 1. الدراسة التقليدية (18 سا)
2. الدراسة المتجهية (16 سا)
3. الدراسة التحليلية (9 سا)
4. التحويلات المستوية (16 سا)
|
التحليل ( التوابع العددية) (42 سا) 1. التعاريف والتمثيل (14 سا)
2. الاتصال والاشتقاق (22 سا)
3. التكامل (6 سا)
حساب المثلثات (15 سا) 1. الخطوط المثلّثية (4 سا)
2. المعادلات المثلثية (7 سا)
3. التوابع الدائرية (4 سا)
الإحصال والإحتمال (20 سا) 1. الإحصاء (8 سا)
2. الاحتمال (12 سا)
|
المحتوى |
|
|
الجبر (20 سا) 1. المرتكزات (10 سا)
2. المعادلات والمتراجحات (10 سا)
التحليل (التوابع العددية) (25 سا) 1. التعاريف والتمثيل (15 سا)
2. النماذج الرياضية لزوم الاقتصاد والعلوم الاجتماعية (10 سا)
|
الإحصاء والإحتمال (15 سا) 1. الإحصاء (10 سا)
2 . الاحتمال (5 سا)
|
المحتوى |
|
|
الجبر (25 سا) 1. المرتكزات (8 سا)
2. الحساب العددي والحرفي (7 سا)
3. المعادلات والمتراجحات (10 سا)
التحليل ( التوابع العددية) (60 سا) 1. التعاريف والتمثيل (20 سا)
2. الاتصال والاشتقاق (5 سا)
3. التكامل (10سا)
4. المعادلات التفاضلية (10 سا)
5. النماذج الرياضية لزوم الاقتصاد والعلوم الاجتماعية (15 سا)
|
الإحصاء والإحتمال (35 سا) 1. الإحصاء (15 سا)
2. الاحتمال (20 سا)
|
المحتوى |
|
|
الجبر (60 سا) 1. المرتكزات (15 سا)
2. الحساب العددي والحرفي (10 سا)
3. المعادلات والمتراجحات (10 سا)
4. الأعداد (25 سا)
الهندسة (90 سا) 1. الدراسة التقليدية (20 سا)
2. الدراسة المتجهية (5 سا)
(
3. الدراسة التحليلية (30 سا)
4. التحويلات المستوية (35 سا)
|
التحليل (التوابع العددية) (105سا) 1. التعاريف والتمثيل (40 سا)
2. الاتصال والاشتقاق (25 سا)
3. التكامل (30 سا)
4. المعادلات التفاضلية (10 سا)
حساب المثلثات (15 سا) 1. الخطوط المثلثية (5 سا)
2. المعادلات المثلّثية (5 سا)
3. التوابع الدائرية (5 سا)
الإحصاء والإحتمال (30 سا) 1. الإحصاء (10 سا)
2. الاحتمال (20 سا)
|
المحتوى |
|
|
الجبر (35 سا) 1. المرتكزات (8 سا)
2. الحساب العددي والحرفي (10 سا)
3. المعادلات والمتراجحات (7 سا)
4. الأعداد (10 سا)
الهندسة (15 سا) 1. الدراسة التحليلية (15 سا)
التحليل (التوابع العددية) (65 سا) 1. التعاريف والتمثيل (25 سا)
2. الاتصال والاشتقاق (15 سا)
3. التكامل (15 سا)
4. المعادلات التفاضلية (10 سا)
|
حساب المثلثات (5 سا) 1. التوابع الدائرية (5 سا)
الإحصاء والإحتمال (30 سا) 1. الإحصاء (10 سا)
2. الاحتمال (20 سا)
|




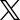
 (س ³ ص).
(س ³ ص). ".
". = 0
= 0 (س
(س  ص).
ص). = 0
= 0 ولـ
ولـ  تطبيقات.
تطبيقات. ،
،  ) = ء(مقاس ط أو 2 ط).
) = ء(مقاس ط أو 2 ط). وَ لـ
وَ لـ  ،
،  ) = ء(مقاس ط أو 2 ط).
) = ء(مقاس ط أو 2 ط). .
.